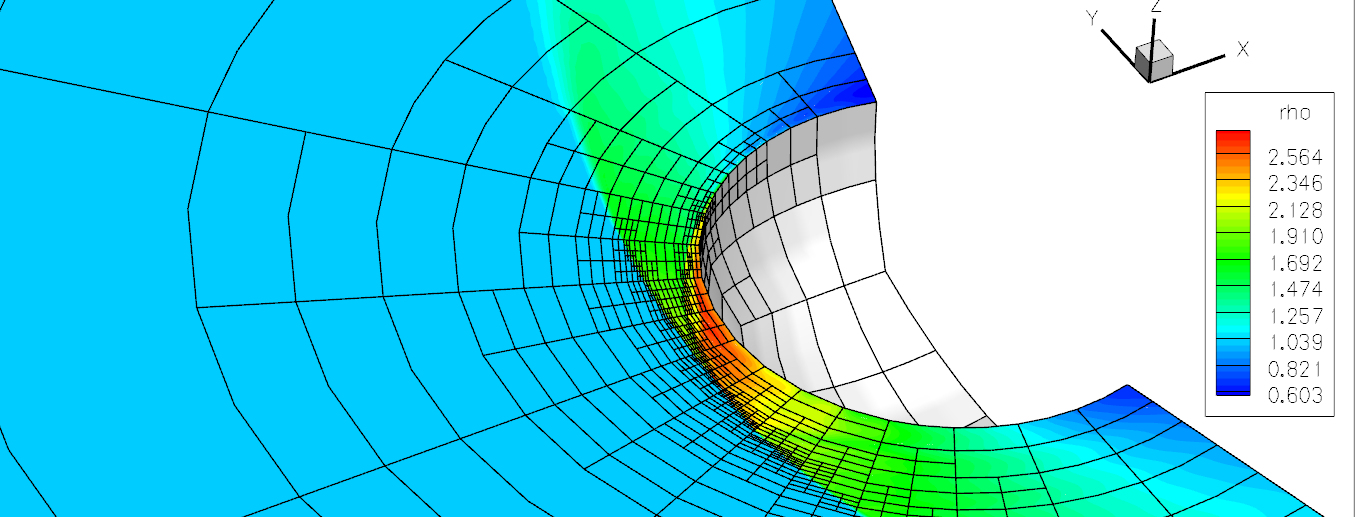
AER310: Gasdynamics
Course Description
Basic introduction to compressible gasdynamics. Includes some fundamental thermodynamics, thermal and caloric equations of state, derivation of Euler’s equations by control volume approach. Also, includes the theory of steady flows in ducts with area changes, adiabatic frictional flows, duct flows with heat transfer, normal and oblique shock waves, Prandtl-Meyer expansion wave, moving shock and rarefaction waves, shock tubes, and wind tunnels. The lectures are supplemented by problem sets. Reference book: Anderson, J.D., Modern Compressible Flow with Historical Perspective.